NBlog - 证明皮克定理

引入

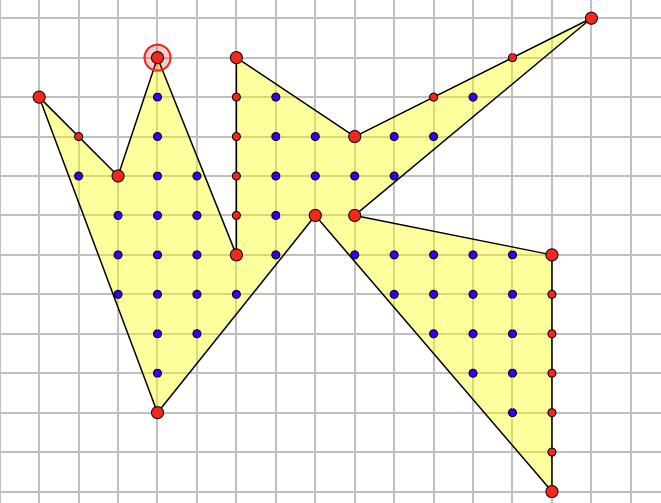
如图所示，图中有一个复杂的多边形，它存在于一个网格中，假设网格每一个的边长都是1，那么，这个多边形的面积 $S$ 是多少呢？

看到这个问题，你可能会优先采用小学老师教过的“大面积减小面积”的方法，但这种方法计算起来比较慢。那么，是否有公式可以直接求解它的面积呢？这看似不可能的公式还真的存在，它就是皮克定理。

皮克定理

对于如上图所示的这样的多边形，它的面积符合如下公式：

S = I + \frac{O}{2} - 1

$I$ 是多边形内部所包含的格点总数
$O$ 是多边形的边所经过的格点总数

以上图的多边形为例，套用公式即可得出面积

S = 45 + \frac{24}{2} - 1 = 56

那么接下来，我们尝试简单证明一下这个公式。

证明

我们不妨先从最简单的情况入手，即求解网格中长方形的面积。

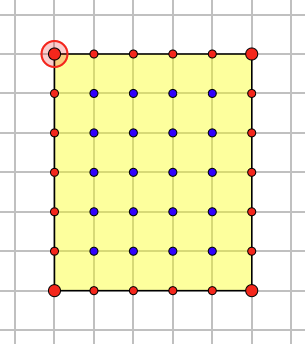一个简单的长方形

由于网格的固有性质，我们可以知道长方形的周长与多边形的边所经过的格点总数 $O$ 是相等的。设长方形的长与宽分别为 $a$ 、 $b$ ，可得

O = 2 * (a + b)

移项，可得

a + b = \frac{O}{2}

接着，我们可以知道，多边形内部所包含的格点总数 $I$ 可以用 $a$ 、 $b$ 来表示，即

(a - 1) (b - 1) = I

化简，得

ab - (a + b) + 1 = I

由 $S = ab$ ，可得

S = I + (a + b) - 1

将 $(1)$ 式代入，即可得出公式

S = I + \frac{O}{2} - 1

那么现在我们就证明了长方形情况下的皮克定理，但皮克定理可用于网格中的任意多边形，所以我们还需要推广这个公式。我们知道，将这样的长方形在网格中进行切割、拼接操作即可获得复杂的多边形，所以我们也可以以此来推广我们刚刚证明出来的公式。

切割时分为多种情况，我们一一分类讨论。

切割线不经过或包括多边形内部的格点

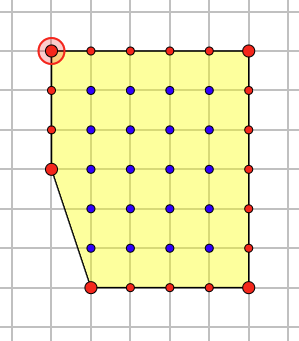示例：切割后的多边形

若切割时切割线不经过或包括多边形内部的格点，那么切割出来的这个三角形必有一边的边长为1。

当我们把长度为1的边拼接在切割后的多边形上，则不会改变 $I$ 和 $O$ 的大小

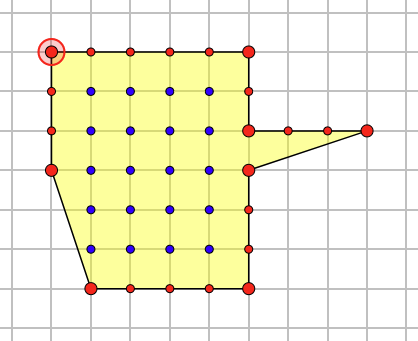示例：拼接后的多边形

设拼接后多边形的边所经过的格点总数为 $O^{'}$ ，则有

O^{'} = O + 2 - 2 = O

故此时的 $O$ 不变。又因为切割线不经过或包括多边形内部的格点，所以 $I$ 也不变。

所以，此时拼接后的图形的面积仍为

S = I + \frac{O}{2} - 1

当我们把长度不为1的另一条边拼接在切割后的多边形上，则 $I$ 和 $O$ 大小改变，但面积不变

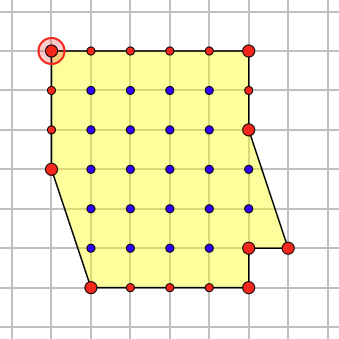示例：拼接后的多边形

设拼接后多边形内部所包含的格点总数及其变化量分别为 $I^{'}$ 、 $Δ I$ ，拼接后多边形的边所经过的格点总数为 $O^{'}$ ，拼接后的面积为 $S^{'}$ ，则有

I^{'} = I + Δ I

假设皮克定理的公式对此时的多边形仍然成立，则有

S^{'} = I^{'} + \frac{O ^{'}}{2} - 1

将 $(2)$ 式代入，可得

S^{'} = I + Δ I + \frac{O ^{'}}{2} - 1

由于网格的固有性质，拼接时多边形内部所包含格点总数的变化量 $Δ I$ 会与所拼接的三角形的边长有如下关系（设所拼接三角形的边的边长为 $x$ ）：

Δ I = x - 1

移项，得

x = Δ I + 1

由于网格的固有性质，拼接后多边形的边所经过的格点总数符合下式：

O^{'} = O + 2 - 2 x

将 $(4)$ 式代入，可得

O^{'} = O + 2 - 2 (Δ I + 1) = O - 2Δ I

将 $(5)$ 式代入 $(3)$ 式，可得

S^{'} = I + Δ I + \frac{O - 2Δ I}{2} - 1

化简，即可得出面积

S^{'} = I + \frac{O}{2} - 1

故

S^{'} = S

假设成立，皮克定理的公式对此时的多边形仍然成立。

综上所述，切割线不经过或包括多边形内部的格点时，皮克定理成立。

切割线经过或包括多边形内部的格点

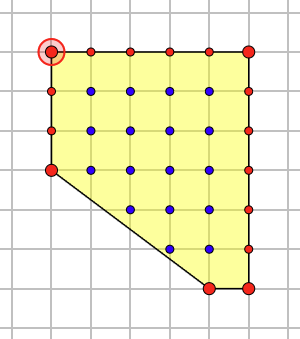示例：切割后的多边形

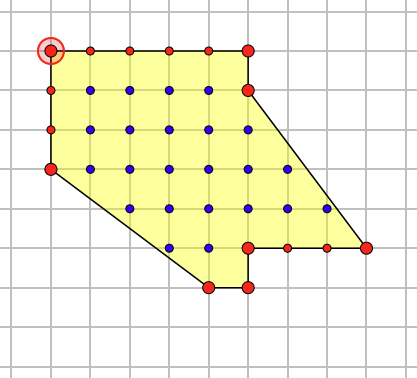示例：拼接后的多边形

设切割下来的三角形中，包含了 $m$ 个格点，所拼接三角形的边的边长为 $x$ ，拼接后多边形内部所包含的格点总数及其变化量分别为 $I^{'}$ 、 $Δ I$ ，拼接后多边形的边所经过的格点总数为 $O^{'}$ ，拼接后的面积为 $S^{'}$ ，切割线所经过的格点数为 $t$ ，则有

I^{'} = I - m + m - t + (x - 1) = I + x - t - 1

I^{'} = I + Δ I

可得

Δ I = I^{'} - I = x - t - 1

x = Δ I + t + 1

假设皮克定理的公式对此时的多边形仍然成立，则有

S^{'} = I^{'} + \frac{O ^{'}}{2} - 1

将 $(6)$ 式代入，可得

S^{'} = I + Δ I + \frac{O ^{'}}{2} - 1

由于网格的固有性质，拼接后多边形的边所经过的格点总数符合下式：

O^{'} = O + 2 (t + 1) - 2 x

将 $(7)$ 式代入，可得

O^{'} = O + 2 (t + 1) - 2 (Δ I + t + 1) = O - 2Δ I

将 $(9)$ 式代入 $(8)$ 式，可得

S^{'} = I + Δ I + \frac{O - 2Δ I}{2} - 1

化简，即可得出面积

S^{'} = I + \frac{O}{2} - 1

故

S^{'} = S

假设成立，皮克定理的公式对此时的多边形仍然成立。

综上所述，切割线经过或包括多边形内部的格点时，皮克定理成立。

结论

我们证明了由长方形切割而来的所有多边形，其面积都符合皮克定理的公式；又因为这样切割而来的多边形囊括了网格中所有的多边形，因此网格中所有的多边形的面积都符合皮克定理：

S = I + \frac{O}{2} - 1

结语

上面的证明过程可能较为简单，毕竟是我自己研究而得的结果，有的地方或许会不严谨，如果你有发现任何错误，欢迎在留言区指出。